STATISTIKA DAN PROBABILITAS : BAB 10

Januari 4, 2014 by agustiannnn in Statistika dan Probabilitas | Tinggalkan komentar

DISTRIBUSI PELUANG/PROBABILITAS II

Sebaran Normal

• Peubah acak X yang menyebar secara normal dengan fungsi kepekatan peluang:

Contoh soal:
Diketahui X menyebar secara normal dengan  = 50 dan  =10. Carilah peluang bahwa X mendapat nilai antara 45 dan 62.
Petunjuk:

Hampiran Normal Terhadap Binom

Bila X peubah acak Binom dengan nilai tengah  = np dan q = 1 – p maka ragam / varians 2 = npq
maka bentuk limit sebaran normal baku:

Contoh soal:
Suatu ujian pilihan ganda terdiri atas 200 soal masing-masing dengan 4 pilihan dan hanya satu jawaban yang benar. Tanpa memahami soal sedikitpun masalahnya dan hanya dengan menerka saja, berapakah peluang seorang mahasiswa menjawab 25 sampai dengan 30 soal dengan benar, untuk 80 dari 200 soal?
Petunjuk :

Contoh Soal.
1. Untuk sebaran normal dengan  = 50 dan  = 10. Hitunglah peluang bahwa X mengambil nilai antara 45 dan 62.

Jawab.

2. Untuk sebaran normal dengan  = 300 dan  = 50. Hitunglah peluang bahwa peubah acak X meng-ambil suatu nilai yang lebih besar dari 362.

Jawab.

3. Diberikan sebuah sebaran normal dengan  = 40 dan  = 6. Hitunglah nilai X yang:
a. Luas daerah dibawahnya ada 38%
b. Luas daerah diatasnya 5%

Jawab.

Penerapan sebaran normal

4. Suatu jenis aki mencapai umur rata-rata 3,0 tahun dengan simpangan baku 0,5 tahun. Bila umur aki itu menyebar normal, hitunglah peluang bahwa sebuah aki tertentu akan mencapai umur kurang dari 2,3 tahun

Jawab.

5. Sebuah perusahaan alat listrik memproduksi bohlam yang umurnya menyebar normal dengan nilai tengah 800 jam dan simpangan baku 40 jam. Hitunglah peluang sebuah bohlam hasil produksi-nya akan mencapai umur antara 778 dan 834 jam.

Jawab.

6. Pada suatu ujian, nilai rata-ratanya adalah 74 dan simpangan bakunya 7. Bila 12% diantara peserta ujian akan diberi nilai A dan nilai itu mengikuti sebaran normal. Berapakah batas nilai terkecil bagi A dan batas nilai tertinggi bagi B?

Jawab.

7. Pada suatu ujian, nilai rata-ratanya adalah 74 dan simpagan bakunya 7. Bila nilai itu mengikuti sebaran normal, tentukan D6 = desil ke 6.

Jawab.

8. Rata-rata tinggi anjing pudel jenis tertentu adalah 30 cm, dan simpangan bakunya 41 cm. Berapa % banyaknya anjing pudel jenis tersebut yg tingginya melebihi 35 cm, bila tinggi itu menyebar normal dan dapat diukur sampai ketelitian berapapun?

Jawab.

9. Rata-rata tinggi anjing pudel jenis tertentu adalah 30 cm, dan simpangan bakunya 4,1 cm. Hitunglah persentase anjing pudel yang tingginya melebihi 35 cm bila tingginya di ukur sampai sentimeter ter-dekat?

Jawab.

10. Nilai mutu rata-rata (NMR) 300 mahasiswa tingkat persiapan mengikuti suatu sebaran normal dengan nilai tengah 2,1 dan simpangan baku 0,8. Berapa banyaknya mahasiswa tersebut yang mencapai NMR antara 2,5 dan 3,5 inklusif bila NMR itu dihitung sampai persepuluhan terdekat.

Jawab.

STATISTIKA DAN PROBABILITAS : BAB 9

Januari 4, 2014 by agustiannnn in Statistika dan Probabilitas | Tinggalkan komentar

Sebaran Normal

• Peubah acak X yang menyebar secara normal dengan fungsi kepekatan peluang:

• Peubah acak normal baku :

Nilai harapan peubah acak X =  dan ragam 2, sedangkan peubah acak Z mempunyai nilai harapan = 0 dan ragam = 1.

Contoh soal:
Diketahui X menyebar secara normal dengan  = 50 dan  =10. Carilah peluang bahwa X mendapat nilai antara 45 dan 62.
Petunjuk:

Contoh soal:
Suatu ujian pilihan ganda terdiri atas 200 soal masing-masing dengan 4 pilihan dan hanya satu jawaban yang benar. Tanpa memahami soal sedikitpun masalahnya dan hanya dengan menerka saja, berapakah peluang seorang mahasiswa menjawab 25 sampai dengan 30 soal dengan benar, untuk 80 dari 200 soal?
Petunjuk :

Jawab.

Penerapan sebaran normal

Jawab.

7. Pada suatu ujian, nilai rata-ratanya adalah 74 dan simpagan bakunya 7. Bila nilai itu mengikuti sebaran normal, tentukan D6 = desil ke 6.

Jawab.

STATISTIKA DAN PROBABILITAS : BAB 8

Januari 4, 2014 by agustiannnn in Statistika dan Probabilitas | Tinggalkan komentar

TEORI PROBABILITAS

PROBABILITAS (PELUANG KEJADIAN)

P(A) = Probabilitas / peluang kejadian A terjadi :

0 £ P(A) £ 1

P(A) = a = banyak cara (kemungkinan) A terjadi

n = semua cara yang mungkin

Probabilitas adalah ukuran peluang terjadinya suatu kejadian dalam suatu percobaan.

Contoh-Contoh :

Dari 240 komponen hasil produksi yang diambil secara acak, terdapat 20 komponen cacat, maka probabilitas cacat :

P(cacat) =

Sebuah dadu dilempar, maka probabilitas muncul genap adalah : {2,4,6}:

P(genap) =

KOMBINASI (urutan tidak diperhatikan ®Tidak perlu ada tempat duduk )

PERMUTASI (urutan diperhatikan ® Ada tempat duduk )

Contoh : Kombinasi 2 huruf dari 3 huruf (A,B,C) vs permutasi 2 huruf dari 3 huruf (A,B,C)

Contoh Penerapan dalam Probabilitas:

Sebuah kartu diambil dari tumpukan 52 kartu bridge (remi), maka probabilitas kartu itu a). AS b). King atau Quin adalah … ?

Jawab: a). P(AS) =

b). P(K atau Q) =

Sebuah kantong berisi 5 kelereng putih dan 12 kelereng biru, maka hitung probabilitas mengambil : a). satu kelereng putih b). satu kelereng putih atau biru c). dua kelereng biru d) dua kelereng: satu putih satu biru

Jawab: a). P(Putih) =

b). P(putih atau biru) = +

c). P(2 biru) =

d). P(1 putih 1 biru) =

Sebuah kotak berisi 10 buah manik, terdiri 6 merah dan 4 putih. Diambil secara acak 3 buah manik. Berapa peluang /probabilitasnya, bila :
1. Semuanya merah
2. Semuanya putih
3. 2 merah, 1 putih
4. 1 merah, 2 putih

Jawab : Banyak cara mengambil 3 manik

₁₀C₃ = = 120 cara

Peluang 3 manik semuanya merah :
Jawab :

A = himpunan penduduk mempunyai TV, ® P(A) =

B = himpunan penduduk mempunyai radio ® P(B) =

AÇB = himpunan penduduk mempunyai TV dan radio P(AÇB) =

Peluang seseorang memiliki TV atau Radio :

AÇB¹Æ ®P(AÈB) = P(A) + P(B) – P(AÇB)

= =
1. Sebuah dadu dilempar berapa peluang muncul angka £ 2 atau ³ 5 ?
Jawab : A =

B =

A Ç B = Æ ® P(AÈB) = P(A) + P(B)

=
1. Sebuah dadu dilempar, berapa peluang muncul angka ¹ 2 ?
Jawab: A =

P(A^c) = 1 – P(A) = 1 –

atau cara lain

B =
1. Dua dadu dilempar. Berapa peluang muncul {4,4} ? Jumlah 4 ? Muncul kembar ?
Jawab : A = {4} ® P(A) =

B = {4} ® P(B) = ; P(4,4)=P(AÇB) = P(A) x P(B) =

Tabel semua kemungkinan bila dua buah dadu dilempar :

Lima balok merah dan 4 balok putih ditaruh berjejer dalam satu baris.

a). Berapa pobabilitas p, jika pada bagian tepi keduanya balok merah ?

b). Berapa pobabilitas p, jika pada bagian tepi satu balok merah satu putih?

Jawab: Total semua kemungkinan 5 balok merah & 4 balok putih berjejer adalah:

a). Bagian tepi keduanya merah adalah =

Sehingga probabilitas pinggir keduanya merah p = 35/126 //

b). Bagian tepi satu balok merah satu balok putih adalah =

= 2.

Jadi probabilitasnya pinggir satu merah satu putih p = 70/126 = 5/9 //

S = {a₁, a₂, a₃, a₄}

P = Fungsi probabilitas pada S

a. Hitung P(a₁), jika P(a₂) = , P(a₃) =, P(a₄) =

a.Hitung P(a₁) dan P(a₂), jika P(a₃) = P(a₄) = dan P(a₁) = 2 P(a₂)

c. Hitung P(a₁), jika P(a₂, a₃) = , P({a₂,a₄}) = dan P(a₂) =

Jawab :

Misal P(a₁) = p, maka

P(a₁)+ P(a₂) + P(a₃) + P(a₄) = 1

p + ++= 1 à p += 1

p = 1 – = P(a₁)

Misal P(a₂) = p, maka P(a₁)= 2p

Sehingga P(a₁)+ P(a₂) + P(a₃) + P(a₄) = 1

2p + p + + = 1 à 3p = à p =

\ P(a₂) = , dan P(a₁) = 2. =

Misal P(a₁) =p

P(a₃) = P({a₂, a₃}) – P(a₂)

= –

P(a₄) = P({a₂, a₄}) – P(a₂)

= –

p + ® p = 1 –

12. Dua buah dadu dilempar 3 kali.

a). Berapa probabilitasnya mendapatkan sekali pelemparan jumlah 9 ?

b). Berapa probabilitasnya mendapatkan dua kali pelemparan jumlah 7 ?

Jawab:

a). Jumlah 9 adalah : (3,6); (4,5); (5,4); (6,3) ada 4 kemungkinan.

Dalam sekali pelemparan dua dadu, prob.= 4/36 = 1/9 (sukses (p))

Probabilitas tidak mendapatkan jumlah 9 = 1 – 1/9 = 8/9 (gagal (q=1-p))

à dua kali pelemparan = ( 8/9 )²

Sekali pelemparan dari 3 pelemparan = ₃C₁

RUMUS BINOMIAL : _nC_x p^x q^n-x

Jadi prob. mendapatkan sekali jumlah 9 = ₃C₁ . (1/9)¹ (8/9)² = 64/243 //

b). Jumlah 7 adalah : (1,6); (2,5); (3,4); (4,3); (5,2); (6,1) ada 6 kemungkinan.

Dalam sekali pelemparan dua dadu, prob.= 6/36 = 1/6 (sukses)

à dua kali pelemparan = ( 1/6 )²

Probabilitas tidak mendapatkan jumlah 7 = 1 – 1/6 = 5/6 (gagal)

à satu pelemparan = ( 5/6 )¹

Dua kali pelemparan dari 3 pelemparan = ₃C₂

Jadi prob. mendapatkan 2 kali jumlah 7 = ₃C₂ . (1/6)² (5/6)¹ = 5/72 //

STATISTIKA DAN PROBABILITAS : BAB 7

Januari 4, 2014 by agustiannnn in Statistika dan Probabilitas | Tinggalkan komentar

ANALISIS DATA

07. Analisis Data Berkala
Data berkala atau data deret waktu adalah sekumpulan data hasil observasi dalam interval waktu tertentu. Untuk menganalisis data yang berbentuk data deret waktu, di gunakan analisis data deret waktu, yang di pengaruhi oleh trend, siklis, musiman dan residu ( T S M R ).
Salah satu kegunaan dari analisis data deret waktu adalah untuk meramalkan keadaan di waktu yang akan datang berdasarkan data waktu yang lalu.

07.1 Trend
Trend atau kecenderungan yaitu gejala gerakan jangka panjang sebagai gerak waktu yang bisa naik dan bisa turun.
Trend adalah garis kecenderungan data. Persamaan garis Trend bisa berupa garis lurus ataupun garis yang melengkung. Trend yang berupa garis lurus disebut trend yang linier dengan persamaan :
Yt = a + b t
Dimana :   a =   konstanta, yang menunjukan titik potong garis trend dengan
sumbu vertikal y
b =   koefisien trend, yang menunjukan tingkat
perkembangan/penurunan
t   =   waktu
Y =   nilai Trend

Membuat persamaan Trend :

07.1.1 Metode Setengah Rata–rata (Semi Average)
Membuat persamaan dengan cara setengah rata-rata pada prinsipnya kita membuat sebuah persamaan matematika dengan titik yang diperoleh dari membagi data menjadi dua bagian, masing-masing setengah dari jumlah data, kemudian di jumlah dan di rata-ratakan

Langkah pembuatannya sebagai berikut :
1. Bagilah deret waktu data menjadi dua bagian yang sama dan tiap bagian harus mempunyai jumlah data yang sama.
2. Jumlahkan nilai data pada tiap-tiap bagian, setelah dijumlah hitung nilai rata-ratanya dan letakkan nilai rata-rata itu pada data (periode) yang ada ditengah.

Contoh :
1. Untuk jumlah data yang genap:
Karena jumlah data genap, maka data bisa dibagi menjadi 2 kelompok
Hasil Penjualan Sebuah Perusahaan Tahun 1991 – 2006
STATISTIKA dan PROBABILITAS
MODUL 07
ANALISIS DATA

Membuat persamaan Trend :

Contoh :
1. Untuk jumlah data yang genap:
Karena jumlah data genap, maka data bisa dibagi menjadi 2 kelompok
Hasil Penjualan Sebuah Perusahaan Tahun 1991 – 2006

Dengan memasukan titik kedalam persamaan Y = a + b t, diperoleh:

Persamaan pertama 107,14 = a + b 1993

Persamaan kedua 164,31 = a + b 2001 –

Dengan eliminasi – 57,17 = – 8 b

b = 7,15

Kemudian nilai b di masukkan kedalam salah satu persamaan

107,14 = a + 7,15 . 1993

a = – 14142.8

Dari nilai di atas, diperoleh persamaan y_t = -14142.8 + 7,15 t

Artinya peningkatan penjualan perusahaan itu setiap tahun sebesar Rp. 7,15 juta.

Untuk meramalkan hasil penjualan pada tahun 2008 à t = 2008 :

Y₂₀₀₈ = -14142,8 + 7,15 . 2008 = 214.4

Artinya penjualan perusahaan itu pada tahun 2008 diperkirakan Rp. 214.4 juta

Dari tabel diatas dapat diperoleh :

dan

Sehingga persamaannya menjadi Y_t = 22,5 + 0,71 t

Artinya peningkatan penjualan perusahaan itu setiap tahun

sebesar Rp. 0,71 juta.

Untuk meramalkan penjualan tahun 2010, dengan koding 23

diperoleh Y₂₀₀₈ = 22,5 + 0,71 . 23 = 38.83

07.2. Musiman

Musiman yaitu perubahan yang berulang-ulang secara periodik dalam selang waktu tertentu
Fluktuasi-fluktuasi sekitar trend yang berulang secara teratur setiap tahun adalah variasi musiman. Variasi ini dapat disebabkan oleh faktor-faktor alam maupun faktor institusional yang akhirnya berpengaruh terhadap kebiasaan-kebiasaan.
Sebagai gambaran, permintaan tekstil meningkat pada saat mendekati hari raya dan pada saat tahun ajaran baru bagi murid-murid SD, SMP, dan SMA. Begitu juga permintaan payung meningkat pada saat musim penghujan datang. Peningkatan permintaan diatas periode waktunya kurang dari satu tahun, mungkin hanya beberapa bulan, setelah itu keadaan permintaan akan kembali seperti biasa.
Manfaat praktis menghitung variasi musiman, yaitu agar lebih realistis dalam menyusun perencanaan dan penjadwalan produksi, sehingga setiap permintaan (jumlah besar/kecil) pada waktu-waktu tertentu dapat dipenuhi dengan baik..

Langkah-langkah dalam menghitung variasi musiman adalah sebagai berikut:

1. Harus ada data berkala dengan periode kurang dari satu tahun (triwulan, bulan, dan lain-lain)
2.    Jumlahkan data tiap periode
3.    Jumlahkan data tiap tahun dan hitung rata-ratanya
4.    Mengetahui indeks musiman.

STATISTIKA DAN PROBABILITAS : BAB 6

Januari 4, 2014 by agustiannnn in Statistika dan Probabilitas | Tinggalkan komentar

REGRESI LINIER GANDA DAN NON LINIER

1. REGRESI LINIER GANDA
Analisis regresi ganda merupakan pengembangan dari analisis regresi sederhana. Kegunaannya yaitu untuk meramalkan nilai variabel terikat (Y) apabila variabel bebasnya (X) dua atau lebih.
Analisis regresi ganda adalah alat untuk meramalkan nilai pengaruh dua variabel bebas atau lebih terhadap satu variabel terikat (untuk membuktikan ada tidaknya hubungan fungsional atau hubungan kausal antara dua atau lebih variabel bebas X1, X2, …., Xi terhadap suatu variabel terikat Y.

Persamaan regresi ganda dirumuskan sebagai berikut :

CARA I.

Dengan persamaan Normal (Supranto, Ed.5 Jilid 1, hal.184)
untuk menghitung a, b1, b2 sbb:

Cara II:

Nilai-nilai pada persamaan regresi ganda untuk dua variabel bebas dapat ditentukan sebagai berikut (STATISTIKA, Ridwan, Sunarto, 2007, hal.109):

CARA I.
Persamaan Garis Regresi (Trend) Linear Berganda dengan dua variabel bebas:

1. Cara I: Perhitungan

Dengan persamaan Normal (Supranto, Ed.5 Jilid 1, hal.184)
untuk menghitung a, b1, b2 sbb:

Contoh Soal cara I:
Suatu penelitian dilakukan terhadap 8 rumah tangga yang dipilih secara
random di sebuah kabupaten, data (pendapatan, jumlah anggota keluarga, dan
pengeluaran) adalah sebagai berikut:

Hitunglah: 1. Trend Linear berganda data tersebut ?

1. Penaksiran pengeluaran minimal (y1) perbulan untuk
Kebutuhan pokok rumah tangga tersebut?

Persamaan Normal:
1)       8   a +   103,5    b1 + 30 b2   =    92
2)   103,5 a + 1367,25 b1 + 391 b2 = 1208
3)    30     a +     391     b1 + 126 b2 =   364

v\:* {behavior:url(#default#VML);}
o\:* {behavior:url(#default#VML);}
w\:* {behavior:url(#default#VML);}
.shape {behavior:url(#default#VML);}

Normal
0

false
false
false

IN
X-NONE
X-NONE

MicrosoftInternetExplorer4

/* Style Definitions */
table.MsoNormalTable
{mso-style-name:”Table Normal”;
mso-tstyle-rowband-size:0;
mso-tstyle-colband-size:0;
mso-style-noshow:yes;
mso-style-priority:99;
mso-style-qformat:yes;
mso-style-parent:””;
mso-padding-alt:0cm 5.4pt 0cm 5.4pt;
mso-para-margin:0cm;
mso-para-margin-bottom:.0001pt;
mso-pagination:widow-orphan;
font-size:10.0pt;
font-family:”Times New Roman”,”serif”;}

1. Trend Linear berganda data tersebut:

y¹ = a + b1 X1 + b2 X2

= 0,1965 + 0,4964 X2 + 1,3017 X2

2. Penaksiran : X1 = 15 & X2 = 4

Y1 = 0,1965 + 0,4964 (15) + 1,3017 (4)

= 0,1965 + 7,446 + 5,2068

= 12,8493 = (Rp.128.493/bulan)

Saldo = Pendapatan – Pengeluaran

= Rp. 150.000, – Rp. 128.493,

= Rp. 21.507, ( Tabungan )

CARA 2.

Y = a + b1X1 + b2X2

I. Perhitungan Skore rata-rata sebagai berikut :

X1 = Σ X1/n = 103,5 / 8 = 12,94

X2 = Σ X2 / n = 30 / 8 = 3,75

Y = Σ Y / n = 92 / 8 = 11,5

II. PerhitunganPenyimpangan ( deviasi ) sebagaiberikut :

1. Σ X1² = Σ X1 ² – ( Σ X1 )² / n

= 1367,25 – ( 103,5)² / 8

= 1367,25 – 1339,03

= 28,22

2. Σ X2² = Σ X2² – ( Σ X2 )² / n

= 126 – ( 30 )² / 8

= 126 – 112,5

= 13,5

3. Σ Y² = Σ Y² – ( Σ Y ) ² / n

= 1104 – ( 92 ) ² / 8

= 1104 – 1058

= 46

4. Σ X1Y = Σ X1Y – ( Σ X1) . ( Σ Y ) / n

= 1208 – (103,5) ( 92) / 8

= 1208 – 1190,25

= 17,75

5. Σ X2Y = Σ X2Y – ( Σ X2) ( ΣY) / n

= 364 – ( 30 ) ( 92 ) / 8

= 364 – 345

= 19

6. Σ X1X2 = Σ X1X2 – ( Σ X1) ( Σ X2) / n

= 391 – (103,5) ( 30) / 8

= 391 – 388,13

= 2,87

( Σ X2 ²) ( ΣX1Y ) – ( Σ X1.X2 ) ( Σ X2Y )

b1 =

( ΣX1² ) ( ΣX2 ² ) – ( Σ X1X2 )²

( 13,5 ) ( 17,75 ) – ( 2,87 ) ( 19 )

(28,22 ) ( 13,5 ) – ( 2,87 )²

= 239,63 – 54,53 = 185,1

380,97 – 8,24 372,73

= 0,4966 = 0, 497

( Σ X1² ) ( ΣX2Y ) – ( Σ X1.X2 ) ( Σ X1Y )

b2 =

( ΣX1² ) ( ΣX2² ) – ( Σ X1X2 )²

( 28,22 ) ( 19 ) – ( 2,87 ) ( 17,75 )

(28,22 ) ( 13,5 ) – ( 2,87 )²

= 536,18 – 50,94 = 485,24

380,97 – 8,24 372,73

= 1,3019 = 1,302.

a = Y – b1X1 + b2X2

= 11,5 – 0,497( 12,94 ) + 1,302( 3,75 )

= 11,5 – 6,43 + 4,88

= 11,5 – 11,31

= 0, 19

1. Trend Linier berganda data tersebut :

Ỳ = a + b1X1 + b2X2

= 0,19 + 0,497 X1 + 1,302 X2

2. Penasiran 2 rumah tangga berikutnya yang mempunyai :

a). X1 = 15 dan X2 = 4

b). X1 = 15 dan X2 = 8

Jawab: a). Penaksiran X1 = 15 dan X2 = 4

Ỳ = 0,19 + 0,497 ( 15 ) + 1,302 ( 4 )

= 0,19 + 7,455 + 5,208

= 12,853 x Rp. 10.000,

= Rp 128.530, ( Saldo = Pendapatan – Pengeluaran )

= Rp. 150.000, – Rp128.530,

= Rp. 21.470, (Tabungan )

b). Penaksiran X1 = 15 dan X2 = 8

Ỳ = 0,19 + 0,497 ( 15 ) + 1,302 ( 8 )

= 18,061 x Rp. 10.000,

= Rp 180.610, ( Saldo = Pendapatan – Pengeluaran )

= Rp. 150.000, – Rp180.610,

= – Rp. 30.610, (Utang)

06.1.1 Tiga variabel bebas:

Nilai-nilai a, b₁, b₂, dan b₃ pada persamaan regresi ganda untuk tiga variabel bebas dapat ditentukan dari rumus-rumus berikut (Sudjana, 2005: hal.348-9):

Contoh untuk regresi 3 variabel dapat dilihat di (Sudjana, 2005: hal.348-9):

4. TREND NON LINEAR KUADRATIK

Trend Kwadratic (Parabola)

Persamaan Garis Trendnya sbb:

y¹ = a + bx+ cx ²

Persamaan ini hampir sama, seperti Trand Linear berganda yaitu:

y¹= a + b1x1 + b2 x2

Dimana: b1 = b x1 = x

b2 = c x2 = x²

Dengan persamaan Normal untuk menghitung :

a, b & c sbb:

v\:* {behavior:url(#default#VML);}
o\:* {behavior:url(#default#VML);}
w\:* {behavior:url(#default#VML);}
.shape {behavior:url(#default#VML);}

Normal
0

false
false
false

IN
X-NONE
X-NONE

MicrosoftInternetExplorer4

Persamaan Normal:

1) 7a + 0 +28 c = 728

2) 0 + 28 b + 0 = 394 → b = 394 = 14,07

3) 28a + 0 + 196c = 2940

Persamaan 1 & 3

1) 7a + 28c = 728 x4

3) 28a + 196c = 2940 x1

Menjadi:

1) 28a + 112c = 2912

3) 28a + 196c = 2940 (-)

0 – 84c = -28

c = -28

= 0,33

-84

Hasil c masukkan ke persamaan 1

7a + 28c = 728

7a + 28 (0,33) = 728

7a = 728 – 9,24

a = 718,76

= 102,68

1. Trend Kwadratic data tsb:

y¹ = a + bx + cx2

= 102,68 + 14,07x + 0,33 x²

2. Penaksiran

a) Th 1991→ xi = 4 → y¹ = 102,68 + 14,07 (4) + 0,33 (4)²

= 102,68 + 56,28 + 5,28

= 164,24

b) Th 1992 → xi = 5 → y¹ = 102,68 + 14,07 (5) + 0,33 (5)²

v\:* {behavior:url(#default#VML);}
o\:* {behavior:url(#default#VML);}
w\:* {behavior:url(#default#VML);}
.shape {behavior:url(#default#VML);}

Normal
0

false
false
false

IN
X-NONE
X-NONE

MicrosoftInternetExplorer4

Persamaan Normal:

1) 6a + 0 + 70c = 93

2) 0 + 70b + 0 = 245 → b = 245 / 70 = 3,5

3) 70a + 0 +1414c = 1277

Persamaan 1 & 3

1) 6a + 70c = 93 x 20,2 (samakan c)

3) 70a + 1414c = 1277 x 1

Menjadi:

1) 121,2a + 1414c = 1878,6

70 a + 1414c = 1277 (-)

51,2 a = 601,6 à a = 601,6/51,2 = 11,75

Hasil a dimasukan ke persamaan 1

6a + 70c = 93

6(11,75) + 70c = 93

70c = 93 – 70,5

c = 22,5 / 70 =0,32

1. Jadi Trend Kwadratik data tersebut adalah :

Y! = a + b X + c X²

= 11,75 + 3,5 X + 0,32 X²

2. Penaksiran :

a. Tahun 1991 Koding Xi = 7

y! = 11,75 + 3,5 (7) + 0,32( 7) ²

= 11,75 + 24,5 + 15,68

= 51,93

b. Tahun 1992 Koding Xi = 9

y! = 11,75 + 3,5 + 0,32( 9)²

= 69,17

v\:* {behavior:url(#default#VML);}
o\:* {behavior:url(#default#VML);}
w\:* {behavior:url(#default#VML);}
.shape {behavior:url(#default#VML);}

1. Dua variabel bebas :

2. Tiga variabel bebas :

3. n variabel bebas :

Normal
0

false
false
false

IN
X-NONE
X-NONE

MicrosoftInternetExplorer4

STATISTIK DAN PROBABILITAS : BAB 5

Januari 4, 2014 by agustiannnn in Statistika dan Probabilitas | Tinggalkan komentar

REGRESI DAN KORELASI LINEAR

1. Pendahuluan

Yang dimaksud regresi dan korelasi disini adalah regresi dan korelasi sederhana yang menguraikan antara satu variabel bebas dengan satu variabel takbebas.

Regresi merupakan alat yang digunakan untuk mengukur pengaruh dari setiap perubahan variabel bebas terhadap variabel tak bebas.
Dengan kata lain digunakan untuk menaksir variabel takbebas ( y ) atas setiap perubahan variabel bebas ( x ).
Analisa korelasi merupakan alat analisis yang dipergunakan untuk mengukur keeratan hubungan antara variabel takbebas ( y ) dengan variabel bebas ( x ) .

2 Analisa Regresi

Tujuan utama melakukan analisa ini dipergunakan untuk membuat prediksi ( ramalan ), dengan menggunakan persamaan regresi linear sederhana   y = a + b x. Didalam persamaan linear ini hubungan antara dua variabel digambarkan secara grafis dalam garis lurus yang disebut garis regresi.
Untuk mencari bentuk persamaan garis regresi   y = a + b x   ini dilakukan langkah-langkah sebagai berikut :
1.   Tentukan yang mana variabel bebas ( x ) dan yang mana variabel takbebas ( y ).
2.   Carilah nilai a dan b dengan menggunakan rumus sebagai berikut :

Contoh :
Setiap biaya promosi yang dikeluarkan oleh suatu perusahaan akan selalu berpengaruh terhadap keuntungan pada tiap tahun.
Dari data suatu perusahaan tertentu diperoleh data dalam jutaan rupiah sebagai berikut :

Tentukanlah :
i. Persamaan garis regresinya
ii. Berapa keuntungan yang diperkirakan jika biaya promosi 10 Juta

Jawab :

– Pertama kita tentukan varibel bebas ( x ) dan variabel takbebas ( y ). Dari data tersebut kita dapat menentukan variabel bebas ( x ) adalah biaya promosi sedangan variabel tak bebas ( y ) adalah keuntungan.
– Buat tabel untuk menghitung nilai b dan a

Jadi persamaan garis regresinya adalah : y = 1,26 + 1,48 x

3. Kesalahan Dalam Ramalan

Setiap pendugaaan rata-rata pasti akan mengalami atau menemukan tingkat kesalahan.
Dalam pendugaan regresi, tingkat kesalahan ini disebut “Standard error of the estimate“.
Untuk menghitung Standard error of the estimate digunakan rumus :

Untuk contoh diatas untuk mencari Standard error of the estimate kita buat tabel sebagai berikut :

4. ANALISA KORELASI

4.1 Pendahuluan

Korelasi adalah suatu alat analisis yang dipergunakan untuk mencari hubungan antara variabel bebas ( x ) dengan variabel takbebas ( y ). Apabila beberapa variabel bebas dihubungkan dengan satu variabel takbebas disebut korelasi berganda, dan apabila satu variabel bebas berhubungan dengan satu variabel takbebas disebut korelasi parsial .
Hubungan antara dua variabel, dapat karena hanya kebetulan saja, dapat pula memang merupakan hubungan sebab akibat. Yang akan dibicarakan dalam modul ini adalah hubungan yang sebab akibat.
Dua varibel berkorelasi apabila perubahan yang lain secara teratur, dengan arah yang sama atau arah yang berlawanan.

4.2. Hubungan Antar Dua Variabel

Arah hubungan antar dua variabel yaitu variabel x sebagai variabel bebas dan variabel y sebagai variabel takbebas dapat dibedakan menjadi tiga yaitu :

1.   Korelasi Positif: korelasi ini menunjukan adanya perubahan pada salah satu variabel yang akan diikuti oleh perubahan variabel yang lain secara teratur dengan arah yang sama. Artinya kenaikan variabel bebas x akan selalu diikuti oleh kenaikan variabel takbebas y, demikian pula sebaliknya.
2.   Korelasi Negatif: korelasi ini menunjukan adanya perubahan pada salah satu variabel yang akan diikuti oleh perubahan variabel yang lain secara teratur dengan arah yang berlawanan. Artinya kenaikan variabel bebas x akan selalu diikuti penurunan variabel takbebas y, demikian pula sebaliknya.
3.   Korelasi Nol: korelasi ini menunjukan ada hubungan yang tak jelas antara satu variabel dengan varibel yang lainnya. Artinya hubungan variabel bebas x dengan variabel takbebas y tidak teratur, kadang arahnya sama kadang arahnya berbeda.

4.3. Kooefisien Korelasi ( r )

Persoalan korelasi akan timbul apabila peneliti dihadapkan dengan pertanyaan apakah ada satu hubungan antar variabel dengan satu variabel yang lain dalam sekumpulan data yang sedang diamati.
Menentukan hubungan antara kedua variabel dinyatakan dengan angka yang bergerak diri –1 sampai dengan +1. Apabila kooefisien korelasi mendekati –1 atau +1 berarti terdapat hubungan yang kuat sebaliknya apabila mendekati nilai 0 maka hubungan kedua variabel tersebut adalah lemah.

4.4. Menentukan Koefisien Korelasi ( r )

Rumus yang umum dipakai untuk menentukan kooefisien korelasi antara peubah x dan peubah y, adalah :
r =

Contoh :
Setiap biaya promosi yang dikeluarkan oleh suatu perusahaan akan selalu berpengaruh terhadap keuntungan pada tiap tahun. Dari data suatu perusahaan tertentu diperoleh data dalam jutaan rupioah sebagai berikut :

Hasil ini menujukan hubungan positif yang sangat kuat yang mempunyai arti bahwa setiap tambahan biaya promosi (x) akan meningkatkan keuntungan perusahaan (y).

Soal :

1. Diketahui : x = % kenaikan biaya iklan, y = % kenaikan hasil penjualan
seperti berikut:

STATISTIKA DAN PROBABILITAS : BAB 4

Januari 4, 2014 by agustiannnn in Statistika dan Probabilitas | Tinggalkan komentar

STATITISKA DAN PROBABILITAS
MODUL 04
ANGKA INDEKS
I. Definisi :
1. Angka Index menggambarkan perubahan-perubahan yang terjadi dari waktu ke waktu pada suatu tempat tertentu, baik harga barang maupun jumlah barang.
2. Pada waktu yang sama terjadi variasi di beberapa tempat yang berbeda.

II. Tujuannya

Untuk perbandingan agar data lebih mudah dimengerti atau dipahami secara kwantitatif,
dalam usaha perencanaan yang lebih matang di masa yang akan dihadapi.

III. Jenis-jenis Angka Index

1.   Index Harga (Index Price ( IP ) )
2.   Index Produksi (Index Quantiti ( IQ ) )
3.   Index Nilai (Index Value ( IV ) )

IV. Waktu Pembuatan Angka Index

Ada 2 macam waktu pembuatan angka Index

1. Waktu Dasar (Base Periode)
Adalah waktu dimana suatu kegiatan (kejadian) digunakan untuk dasar perbandingan

2. Waktu yang bersangkutan
Adalah waktu dimana suatu kegiatan akan dibandingkan dengan waktu dasar.

Contoh:
Produksi padi di Sulawesi Selatan sbb:
Tahun 1990 = 100 ton
Tahun 1991 = 150 ton

Jadi Index Produksi 1991 /1990 = 150 /100 x 100 % = 150 %
Terdapat Kenaikan sebesar : 150 % – 100 % = 50 %

Akan tetapi : bila tahun 1991 produksinya 75 ton
maka index produksi tahun 1991 = 75/ 100 x 100 % = 75 %
Terdapat penurunan 75 % – 100 % = – 25 %

Kesimpulan :
1. Angka Index lebih dari 100 % terjadi kenaikan
2. Angka Index kurang dari 100% terjadi penurunan

1. Drobisch (membuat Rata-rata Laspeyres dan Paasche)

a. DP = LP + PP
2

b. DQ = LQ + PQ
2

2. Marshal Edgeworth

IME = ∑ Pn x ½ (Qo + Qn)
x 100 % atau:
∑ Po x ½ (Qo + Qn)
= ∑ Pn (Qo + Qn)
x 100 %
∑ Po (Qo + Qn)

A1. INDEX SEDERHANA

Dimana:

IP = Index Price (IH = Index Harga)

Pn = Harga pada waktu ke n atau t

Po = Harga waktu Dasar

Contoh:

Harga Rata hasil pertanian beberapa pedagang besar di Jakarta tahun 1970 – 1974 (dalam

Rp/100 Kg), sebagai berikut :

Penyelesaian :

942

1. IQ 1981/ 1980 = X 100% = 95,83 % → Turun = 4,17 %

983

961

2. IQ 82/80 = X 100 % = 97,76 % → Turun = 2,24 %

983

992

3. IQ 83/80 = X 100 % = 100,92 % → Naik = 0,92 %

983

1044

4. IQ 84/80 = X 100 % = 106,21 % → Naik = 6,21 %

983

IVA = X 100 % = 137,14 % – 100 % = 37,14 % (Naik)

IV B = X 100 % = 250 % – 100 % = 150 % (Naik)

IV C = X 100 % = 300 % – 100 % = 200 % (Naik)

A2. INDEX GABUNGAN

∑ Pn

IP = X 100%

∑ Po

∑ Qn

IQ = X 100%

∑ Qo

∑ Pn . Qn

IV = X 100%

∑ Po. Qo

∑ Pn 19

IP = X 100% = X 100 % = 135,71 % -100%

∑ Po 14 = 35,71% (Naik)

∑ Qn 26

IQ = X 100 % = X 100 % = 118,18 % – 100 %

∑ Qo 22 = 18,18 % ( Naik)

∑ Pn . Qn 130

IV = X 100 % = X 100 % = 158,54 % – 100 %

∑ Po . Qo 82 = 58,54 % (Naik)

B. INDEX DITIMBANG

Meliputi :

LASPEYRES

∑ Pn . Qo

a. LP = x 100 %

∑ Po . Qo

∑ Qn . Po

b. LQ = x 100 %

∑ Qo . Po

PAASCHE

∑ Pn .Qn

a. PP = x 100 %

∑ Po . Qn

∑ Qn . Pn

b. PQ = x 100%

∑ Qo . Pn

LASPEYRES

LP = ∑Pn.Qo / ∑ Po.Qo x 100 %

= 70 / 53 x 100% = 132,08 %

LQ = ∑ Po.Qn / ∑ Po.Qo x 100 %

= 62 / 53 x 100 % = 116, 98 %

PAASCHE
1. PP = ∑ Pn.Qn / ∑ Po.Qn x 100%

= 87 / 62 x 100%

= 140, 32 %

PQ = ∑ Pn.Qn / ∑ Pn.Qo x 100 %

= 87 / 70 x 100 %

= 124, 29 %

IRVING FISHER

a. FP = LP x PP = 132, 08 x 140, 32 % = 136, 14 %

b. FQ = LQ x PQ = 116, 98 x 124,29 % = 120, 58 %

DROBISCH

a. DP = LP + PP = 132,08 + 140,32 = 136,2 %

2 2

b. DQ = LQ + PQ = 116,98 + 124, 29 = 120,64 %

2 2

5. Index Value = (Ditimbang )

IV = ∑ Pn.Qn / ∑ Po.Qo x 100 %

= 87 / 53 x 100 %

= 164,15 %

6. INDEX MARSHAL EDGEWORTH

Dasar pertimbangannya adalah rata-rata Produksi(Quantity) dari waktu dasar dan

Waktu tertentu.

∑ Pn. x ½ ( Qo + Qn )

IME = x 100 %

∑Po x ½ ( Qo + Qn)

= ∑ Pn (Qo + Qn ) x 100 %

∑ Po (Qo + Qn )

( 70 + 87 )

= x 100 %

(53 + 62 )

= 157 x 100 %

115

= 137 %

STATISTIKA DAN PROBABILITAS : BAB 3

Januari 4, 2014 by agustiannnn in Statistika dan Probabilitas | Tinggalkan komentar

STATISTIK & PROBABILITAS

MODUL 03

UKURAN SIMPANGAN, DISPERSI DAN VARIASI

M03.1 PENDAHULUAN

Kecuali ukuran gejala pusat ( Mean, Median, Modus ) dan ukuran letak ( Kuartil 1, 2, dan 3 ) masih ada lagi ukuran lain yaitu: ukuran simpangan atau ukuran dispersi. Ukuran-ukuran ini sering dinamakan ukuran variasi, yaitu ukuran yang menggambarkan bagaimana berpencarnya data kuantitatif.

Ukuran dispersi yang akan dibahas antara lain: rentang, rentang antar kuartil, simpangan kuartil atau deviasi kuartil, rata-rata simpangan atau rata-rata deviasi, simpangan baku atau deviasi standar, varians dan koefisien variasi.

M03.2 RENTANG, RENTANG ANTAR KUARTIL DAN SIMPANGAN KUARTIL

Rentang = data terbesar – data terkecil

Rentang hanya dapat dihitung untuk data tanpa kelas, jadi dapat dicari data terbesar dan yang terkecil. Untuk memudahkan pencarian data terkecil dan terbesar, data dapat terlebih dulu disortir ( diurutkan dari kecil ke besar ).

Rentang Antar Kuartil (RAK) adalah selisih antara Kuartil Atas ( K₃ ) dengan Kuartil Bawah ( K₁ ).

RAK = K₃ – K₁

Simpangan Kuartil ( SK ) atau Deviasi Kuartil atau disebut juga Rentang Semi Antar Kuartil harganya adalah setengah dari Rentang Antar Kuartil:

SK = ½ SK = ½ ( K₃ – K₁)

M03.3 SIMPANGAN RATA-RATA

Jika selisih setiap datum x_i dengan Mean (Rata-rata) di tulis | x_i–| untuk i = 1, 2, …n dijumlahkan, kemudian dibagi banyaknya data n, maka menghasilakn Simpangan Rata-Rata (SR), ditulis

SR = i = 1, 2, … n

M03.3 SIMPANGAN BAKU ( DEVIASI STANDAR ) ( S )

S = simpangan baku untuk sampel

= ( baca sigma ) adalah simpangan baku untuk populasi

Varians = S² untuk sampel, Varians = ² untuk populasi.

Berikutnya, apabila sampel telah disusun dalam distribusi frekuensi, maka rumus S² menjadi:

( Disarankan untuk memakai rumus ke II )

Apabila data disusun dalam distribusi frekuensi berkelas, maka x_i adalah nilai tengah dari masing-masing kelas.

Hasil yang diperoleh berbeda dengan di atas, karena telah mengalami pembulatan,

Jadi hasil S² = 172,1 lebih teliti daripada hasil S² = 170,9.

Menghitung varians S² dengan penyederhanaan (sandi):

Dipilih f_i tertinggi, berarti dipilih A = 75,5, dan karena p = 10 jadi c_i = , sehingga :

1). Jika tiap nilai data x_i,ditambah atau dikurangi dengan bilangan yang sama,

maka simpangan baku S tidak berubah.

2). Jika tiap nilai data x_i,dikalikan dengan bilangan yang sama d,

maka simpangan baku yang baru menjadi d kali simpangan baku asal.

MEAN DAN SIMPANGAN BAKU GABUNGAN

Jika ada k buah subsample dengan keadaan seperti berikut:

– Subsample 1: berukuran n₁dengan mean dan simpangan baku s₁

– Subsample 2: berukuran n₂dengan mean dan simpangan baku s₂

………………………………………………………………………………….

– Subsample k: berukuran n_kdengan mean dan simpangan baku s_k

Yang digabung menjadi sebuah sampel berukuran n = n_{1 +}n_{2 + ……… +}n_k, maka

M03.4 BILANGAN BAKU DAN KOEFISIEN VARIASI

Misalkan kita mempunyai sebuah sampel berukuran n dengan data x₁, x₂, …, x_n

sedangkan mean = dan simpangan baku = s. Dari hal-hal di atas dibentuk data

baru z₁, z₂, …, z_n dengan rumus :

z_i = untuk i = 1, 2, …. n

Data baru z₁, z₂, …, z_n ternyata mempunyai mean = 0 dan simpangan baku s = 1.

Untuk data baru yang mempunyai mean dan simpangan baku s₀ ,

dibentuk dengan rumus:

z_i = + s₀ untuk i = 1, 2, …. N

Data baru bilangan z ini sering disebut bilangan standar.

M03.5 DISTRIBUSI FREKUENSI dan KEMIRINGAN

M03.5.3. MODEL POPULASI

Poligon frekuensi yang merupakan garis patah-patah didekati oleh sebuah lengkungan halus yang bentuknya secocok-mungkin dengan bentuk poligon tersebut. Lengkungan yang didapat dinamakan kurva frekuensi.

Jika semua data dalam populasi dikumpulkan, lalu dibuat distribusi frekuensinya, maka kurva frekuensinya dapat menjelaskan sifat karakteristik populasi.

Kurva Normal selalu Simetrik, tapi tidak sebaliknya.

Pada Kurva Positif dan kurva negatif ada hubungan seperti berikut

Model Kurva Positif menggambarkan bahwa terdapat sedikit gejala yang bernilai makin besar. Sedangkan Kurva Negatif terjadi sebaliknya.

Soal ujian yang terlalu mudah, mengakibatkan banyak peserta ujuan yang mendapat nilai baik. Ini menggambarkan Kurva Negatif. Sebaliknya soal ujian yang terlalu sukar, hanya sedikit yang mendapat nilai baik.

M03.5.4. KEMIRINGAN

Kurva positif disebut juga kurva miring ke kiri, artinya kurvanya mempunyai ekor memanjang ke sebelah kanan.

Sebaliknya, kurva negative disebut juga kurva miring ke kanan, artinya kurvanya mempunyai ekor memanjang ke sebelah kiri.

Dalam keadaan kedua hal tersebut di atas, artinya kurvanya tak simetri.

Untuk mengetahui derajat tak simetri kurva, digunakan ukuran kemiringan seperti berikut ini:

Kemiringan = , ukuran kemiringan Pearson Tipe Pertama.

Kemiringan = , ukuran kemiringan Pearson Tipe Kedua.

M03.5.5. KURTOSIS

Kurtosis atau peruncingan selalu dikaitkan dengan kurva normal.

Lepto kurtik adalah kurva yang terlihat lebih runcing dengan kurva normal.

Meso kurtik adalah kurva yang terlihat mendekati kurva normal.

Plati kurtik adalah kurva yang terlihat lebih datar dari pada kurva normal.

Kriteria yang didapat dari rumus ini adalah :

a). a₄= 3 à distribusi normal

b). a₄> 3 à distribusi lepto kurtik

a). a₄= 3 à distribusi plati kurtik

Untuk menyelidiki apakah distribusi normal atau tidak, sering pula dipakai ukuran koefisien kurtosis persentil, diberi symbol Қ ( baca Kappa ), rumusnya:

Kedua gambar di atas (kurva berbentuk J) memperlihatkan fenomena kejadian dalam dunia ekonomi, industry, bursa saham dan fisika. Suatu saat harga-harga naik terus. Suatu saat harga-harga turun terus. Misal pada harga-harga saham di bursa saham di suatu hari, kadang-kadang naik terus, tapi di hari berkutnya turun terus. Contoh lain: sering terjadi harga-harga kebutuhan pokok naik terus menjelang Idul Fitri.

STATISTIKA DAN PROBABILITAS : BAB 2

Januari 4, 2014 by agustiannnn in Statistika dan Probabilitas | Tinggalkan komentar

STATISTIKA & PROBABILITAS

Modul 02

LANJUTAN A). DATA TAK BERKELOMPOK

KUARTIL : Harga / nilai yang membagi data menjadi empat bagian yang sama, setelah

data diurutkan kecil ke besar.

Desil i = 1 , 2 , 3. n 4

à K₂ = 2 K₁à K₃ = 3 K₁

Contoh-contoh:

a). Data 4, 6, 7, 8, 10, 10, 11 à n = 7

à K₁ = data ke = data ke 2 = 6,

à K₂ = data ke 2 K₁ = data ke 4 = 8,

à K₃ = data ke 3 K₁ = data ke 6 = 10

b). Data 4, 6, 7, 8, 10, 10, 11, 11 à n = 8

à K₁ = harga ke = harga ke 2 ¼ = 6 + ¼ (7-6) = 6 ¼

à K₂ = harga ke 2 K₁ = harga ke 4 ½ = 8 + ½ (10-8) = 9

à K₃ = harga ke 3 K₁ = harga ke 6 ¾ = 10 + ¾ (11-10) = 10 ¾

DESIL : Harga / nilai yang membagi data menjadi sepuluh bagian yang sama, setelah

data diurutkan kecil ke besar.

Desil i = 1 , 2 , 3 , …… 9. n 10

à D₂ = 2 D₁à D₃ = 3 D₁ à ……..……à D₉ = 9 D₁

Cara-cara perhitungan Desil sama dengan cara-cara pada perhitungan

Kuartil.

PERSENTIL : Harga / nilai yang membagi data menjadi seratus bagian yang sama,

setelah data diurutkan kecil ke besar.

Desil i = 1 , 2 , 3 , …… 99.

à P₂ = 2 P₁à P₃ = 3 P₁ à ………..…à P₉₉ = 99 P₁

Cara-cara perhitungan Persentil sama dengan cara-cara perhitungan pada

Kuartil.

RATA-RATA UKUR ( U )

Jika diketahui data: x₁, x₂, x₃,………………… x_n, maka rata-rata ukurnya adalah

U =

Contoh: Jika diketahui data: 2, 4, 8, maka rata-rata ukurnya adalah

U = = = 4

RATA-RATA HARMONIK ( H )

Jika diketahui data: x₁, x₂, x₃,………………… x_n, maka rata-rata harmoniknya adalah

H =

Contoh: Jika diketahui data: 2, 4, 8, maka rata-rata harmoniknya adalah

H = = = = 3,43

Contoh penerapan pada soal:

Ali pergi dari kota A ke kota B dengan kecepatan rata-rata 10 km/jam.

Pulangnya dari kota B ke kota A dengan kecepatan rata-rata 20 km/jam.

Ditanyakan: berapa kecepatan rata-rata Ali pergi-pulang ?

Jawab:

Kecepatan Ali pergi-pulang adalah kecepatan harmonik:

H = = = = 13 km/jam

B. DATA BERKELOMPOK

B.1. DATA BERKELOMPOK TANPA KELAS

Data nilai mata kuliah Statistik

No. Urut	Nilai ( x_i)	Frekuensi (f_i )	f_ix_i
1	35	1	35
2	45	2	90
3	55	5	275
4	65	15	975
5	75	25	1875
6	85	20	1700
7	95	12	1140

	Jumlah	80	6090

Mean = = = 76,125

Median = ½ ( data ke 40 + data ke 41 ) = ½ ( 75 + 75 ) = 75

Modus = data baris ke 5 = 75

Kuartil: K₁ =data ke = data ke 20 ¼ = 65 + ¼ (65-65) = 65

K₂ =data ke 2 K₁= data ke 40 ½ = 75+ ½ (75-75) = 75

K₃ =data ke 3 K₁= data ke 60 ¾ = 85+ ½ (85-85) = 85

B.2. DATA BERKELOMPOK DENGAN KELAS

Data nilai mata kuliah Statistik

No	Kelas Nilai	Frekuensi (f_i )	Nilai Tengah (x_i)	f_ix_i
1	31 – 40	1	35,5	35,5
2	41 – 50	2	45,5	91,0
3	51 – 60	5	55,5	277,5
4	61 – 70	15	65,5	982,5
5	71 – 80	25	75,5	1887,5
6	81 – 90	20	85,5	1710,0
7	91 – 100	12	95,5	1146,0
	LebarKelas=10
	Jumlah	n = 80	–	6.130,0

Mean = = = 76,62

Median = b + p ( )

= 70,5 + 10 ( ) = 70,5 + 10 ( ) = 70,5 + 6,8 = 77,3

b = batas bawah kelas median, ialah kelas di mana median terletak

p = panjang atau lebar kelas dimana median terletak

n = banyaknya data

F = jumlah semua frekuensi di bawah kelas median

f = frekuensi kelas di mana median berada

Modus = b + p ( ) = 70,5 + 10 ( ) = 70,5 + 10 ( ) = 70,5 + 6,67 = 77,17

b = batas bawah kelas modus, ialah kelas di mana modus terletak

p = panjang atau lebar kelas dimana modus terletak

b₁ = selisih frekuensi kelas modus dengan frekuensi kelas sebelumnya

b₂ = selisih frekuensi kelas modus dengan frekuensi kelas sesudahnya

Kuartil: K_i = b + p ( ) i = 1, 2, 3

b = batas bawah kelas kuartil, ialah kelas di mana kuartil terletak

p = panjang atau lebar kelas dimana kuartil terletak

n = banyaknya data

F = jumlah semua frekuensi di bawah kelas kuartil

f = frekuensi kelas di mana kuartil berada

K₁ = data ke = data ke 20

K₁ = b + p ( ) = 60,5 + 10 ( ) = 60,5 + 10 ( 0,8 ) = 68,5

K₂ =data ke 2 K₁= data ke 40

K₂ = b + p ( ) = 70,5 + 10 ( ) = 70,5 + 10 ( 0,68 ) = 77,3

K₃ = …. ?

Desil: D_i = b + p ( ) i = 1, 2, 3, …… 9

b = batas bawah kelas desil, ialah kelas di mana desil terletak

p = panjang atau lebar kelas dimana desil terletak

n = banyaknya data

F = jumlah semua frekuensi di bawah kelas desil

f = frekuensi kelas di mana desil berada

D₁ = data ke = data ke 8

D₂ =data ke 2 D₁= data ke 16

D₂ = b + p ( ) = 60,5 + 10 ( ) = 60,5 + 10 ( 0,53 ) = 65,8

D₃ = …. ? D₄ = …. ? D₅ = …. ? …………….. D₉ = …. ?

B.3. DATA BERKELOMPOK DENGAN PENYEDERHANAAN

Dipilih f_i tertinggi, berarti dipilih A = 75,5, jadi c_i =

Maka Mean = A + p ( )

Data nilai mata kuliah Statistik

No	Kelas Nilai	Frekuensi (f_i )	Nilai Tengah (x_i)	c_i	f_ic_i
1	31 – 40	1	35,5	– 4	– 4
2	41 – 50	2	45,5	– 3	– 6
3	51 – 60	5	55,5	-2	– 10
4	61 – 70	15	65,5	-1	– 15
5	71 – 80	25	75,5	0	0
6	81 – 90	20	85,5	1	20
7	91 – 100	12	95,5	2	24
	LebarKelas=10
	Jumlah	n = 80	–	–	9

Mean

= A + p ( )

= 75,5 + 10 ( ) = 75,5 + 1,125 = 76,625

STATISTIKA DAN PROBABILITAS : BAB 1

Januari 4, 2014 by agustiannnn in Statistika dan Probabilitas | Tinggalkan komentar

STATISTIKA & PROBABILITAS

Pengertian statistik, statistika, populasi, sampel dll.

Penyajian data: Diagram-diagram
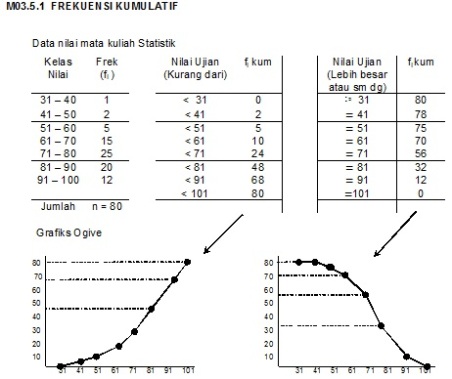
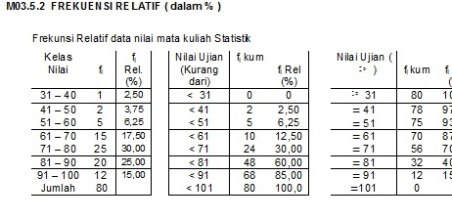
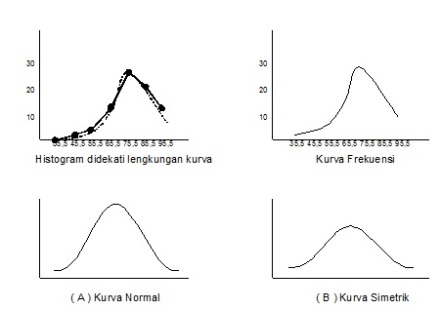
Distribusi frekuensi dan grafiksnya
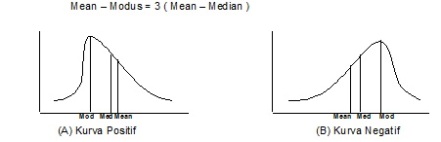
Mean, Median, Modus, Kuartil

Statistik : adalah data berupa catatan angka-angka jumlah atau banyaknya sesuatu dari hasil perhitungan atau penelitian.

Contoh : Statistik nilai ujian mahasiswa, statistik data penduduk dll.

Statistika: adalah pengetahuan seluk-beluk statistik termasuk pengumpulan dan pengolahan data.

Statistika induktif: adalah statistika yang mengolah data sampai diperoleh kesimpulan.

Statistika deskriptif: adalah statistika yang hanya mengolah data saja tanpa mengambil kesimpulan akhir.

Populasi: adalah obyek keseluruhan yang akan diamati.

Sampel: adalah sebagian dari obyek yang diamati, yang menjadi contoh.

Sensus: yaitu penghitungan pengumpulan data secara keseluruhan.

Sampling: adalah proses pengumpulan & pengolahan data yang dilakukan pada sampel.

Macam-macam data:

Data statistik, data kuantitatif, data kualitatif,

data intern, data ekstern, data primer,

data sekunder, data mentah, data diskrit,

data kontinu.

Macam-macam Statistik:

Statistik Pendidikan Statistik Nilai Ujian

Satistik Penduduk Statistik Kelahiran

Statistik Kematian Statistik Kesehatan

Statistik Perusahaan Statistik Jam Lembur

Statistik Pertanian Statistik Kecelakaan, dll.

Statistik Pendidikan

di Kelurahan: ………….. bulan: Agustus 2000

Jenjang	Laki-laki	Wanita	Jumlah
SD
SLP
SLA
UNIV

Statistik Penduduk

di Jakarta: ………….. bulan: Agustus 2000

Walikota	Laki-laki	Wanita	Jumlah
JakPus
JakTim
Jakbar
JakSel

Statistik Nilai Ujian

Mata Kuliah: ………….. Semester: …..

Nilai Ujian	Kode	Jumlah Mahasiswa
0 – 44	E
45 – 55	D
56 – 61	C
62 – 67	C⁺
68 – 73	B
74 – 79	B⁺
80 – 100	A

Statistik Jam Lembur:

Banyaknya jam lembur tiap minggu oleh pekerja-pekerja suatu pabrik adalah:

45 31 46 25 57 39 42 55 20 37

40 59 11 38 34 22 62 33 48 43

57 37 43 51 29 41 35 66 45 32

44 47 42 46 54 65 17 35 53 27

38 22 33 39 45 32 43 41 57 45

Statistik Jam lembur dalam data berkelompok:

Perusahaan: ………..

Jam Lembur	Turus	Jumlah Pegawai
10 – 19	//	2
20 – 29	//// /	6
30 – 39	//// //// ////	14
40 – 49	//// //// //// //	17
50 – 59	//// ///	8
60 – 69	///	3

PENYAJIAN DATA

Diagram dan Grafiks

1. Diagram batang

2. Diagram garis / grafiks ( lurus / patah / lengkung )

3. Diagram Lambang

4. Diagram lingkaran

5. Diagram Peta

6. Diagram pencar / titik

3. Diagram Lambang: dengan menggunakan lambang-lambang.
Lambang gambar orang, bila untuk statistik banyaknya orang.
Lambang gambar mobil, bila untuk statistik banyaknya mobil, dst.

5. Diagram Peta
Berupa peta-peta daerah dengan tanda-tanda tertentu.

MEAN, MEDIAN, MODUS, KUARTIL

A. Data tidak berkelompok: x1, x2, x3, …………… xn

Mean : adalah harga rata-rata.

– x1 + x2 + ……… +
x = n = 1/n ∑ xi

– f1 x1 + f2 x2 + ……… + fn xn
x = n = 1/n ∑ fi xi ,

fi = frekuensi data ke i, i = 1, 2, 3, … n

    Contoh 1: Carilah Mean dari data: 4, 6, 7, 8, 10, 10, 11.
              Jawab: Mean = 1/7 (4 + 6 + 7 + 8 + 10 + 10 + 11)
                        = 1/7 ( 56 ) = 8

    Contoh 2: Carilah Mean dari data: 4, 6, 6, 7, 7, 8, 8, 8, 10, 10.
              Jawab: Mean = 1/10 (1.4 + 2.6 + 2.7 + 3.8 + 2.10 )
                        = 1/10 ( 4 + 12 + 14 + 24 + 20 ) =
        = 1/10 ( 74 ) = 7,4 //

Median: adalah harga tengah.dari data setelah diurutkan dari kecil ke besar.

Jika banyaknya data n ganjil, maka Median adalah harga yang di
tengah-tengah atau data yang ke (n+1)/2

Jika banyaknya data n genap, maka Median adalah harga yang di
tengah-tengah di antara data yang ke n/2 dan data yang ke (n+1)/2.

    Contoh 1: Carilah Median dari 7 data: 4, 6, 7, 8, 10, 10, 11.
           Jawab: Median = data ke (7 + 1)/2 = data ke 4 = 8 //

    Contoh 2: Carilah Median dari 8 data: 4, 6, 7, 8, 10, 10, 11, 11.
           Jawab: Median = harga tengah di antara data ke 8/2 dan
data ke (8/2 + 1)   atau
= harga tengah di antara data ke 4 dan ke 5
= ½ ( 8 + 10 ) = 9 //

Modus: adalah harga / nilai yang paling sering muncul, atau
harga / nilai pada frekuensi tertinggi.

    Contoh-contoh:
    a). Data 4, 6, 7, 8, 10, 10, 11 mempunyai modus = 10.
    b). Data 4, 6, 7, 8, 10, 10, 11, 11 mempunyai modus = 10 dan 11.
    c). Data 4, 6, 6, 8, 10, 10, 11, 11 mempunyai modus = 6, 10 dan 11.
    d). Data 4, 6, 6, 4, 10, 10, 11, 11 tidak mempunyai modus.
    e). Data 4, 6, 7, 8, 9, 10, 11, 12 juga tidak mempunyai modus.

Kuartil: adalah harga / nilai yang membagi data menjadi empat bagian,
Setelah data diurutkan dari kecil ke besar.

Rumus Kuartil:

Ki = data / harga / nilai ke i = 1, 2, 3, …….n, n≥4

    Contoh-contoh:
    a). Data 4, 6, 7, 8, 10, 10, 11  K1 = data ke 2 = 6, K2 = data ke 4 = 8,
    K3 = data ke 6 = 10
    b). Data 4, 6, 7, 8, 10, 10, 11, 11  K1 = harga ke 2 ¼ = 6 + ¼ (7-6) = 6 ¼
     K2 = harga ke 4 ½   = 8 + ½ (10-8) = 9
     K3 = harga ke 6 ¾    = 10 + ¾ (11-10) = 10 ¾
    c). Data 4, 6, 6, 8, 10, 10, 11, 11, 12  K1 = …? , K2 = …? , K3 = …? ,
    d). Data 4, 6, 6, 4, 10, 9, 11, 11  K1 = …? , K2 = …? , K3 = …? ,
    e). Data 4, 6, 7, 8, 9, 10, 11, 12, 13, 14  K1 = …? , K2 = …? , K3 = …? ,

STATISTIKA & PROBABILITAS
Dosen : Drs. Sumardi Hs., M.Sc.
3 sks

Modul 01
Pendahuluan

Lingkup Bahasan:
•   Pokok-pokok kuliah:
o   Pengertian statistik, statistika, populasi, sampel dll.
o   Penyajian data: Diagram-diagram
o   Distribusi frekuensi dan grafiksnya
o   Mean, Median, Modus, Kuartil
o   Simpangan-Simpangan (Kuartil, Baku dll.)
o   Permutasi
o   Kombinasi
o   Binomial
o   Peluang
o   Distribusi Peluang
o   Distribusi Sampling
o   Uji Hipotesis

Buku Utama:
•   Buku yang digunakan sebagai pegangan mahasiswa dan dosen:
o   Prof. DR. Sudjana, M.A, M.Sc. : METODA STATISTIKA, Penerbit TARSITO Bandung.
o
o   Schaum’s : PROBABILITY & STATITICS, McGraw-Hill, New-York
o
o   K A Stroud, Erwin Sucipta : MATEMATIKA UNTUK TEKNIK, Penerbit Erlangga, Jakarta..

Pengertian statistik, statistika, populasi, sampel dll.
o   Penyajian data: Diagram-diagram
o   Distribusi frekuensi dan grafiksnya
o   Mean, Median, Modus, Kuartil

Statistik : adalah data berupa catatan angka-angka jumlah atau banyaknya sesuatu dari hasil perhitungan atau penelitian.

Contoh : Statistik nilai ujian mahasiswa, statistik data penduduk dll.

Statistika: adalah pengetahuan seluk-beluk statistik termasuk pengumpulan dan pengolahan data.

Statistika induktif: adalah statistika yang mengolah data sampai diperoleh kesimpulan.

Statistika deskriptif: adalah statistika yang hanya mengolah data saja tanpa mengambil kesimpulan akhir.

Populasi: adalah obyek keseluruhan yang akan diamati.

Sampel: adalah sebagian dari obyek yang diamati, yang menjadi contoh.

Sensus: yaitu penghitungan pengumpulan data secara keseluruhan.

Sampling: adalah proses pengumpulan & pengolahan data yang dilakukan pada sampel.

Macam-macam data:

Data statistik,        data kuantitatif,    data kualitatif,
data intern,        data ekstern,        data primer,
data sekunder,    data mentah,        data diskrit,
data kontinu.

Macam-macam Statistik:

Statistik Pendidikan        Statistik Nilai Ujian
Satistik Penduduk       Statistik Kelahiran
Statistik Kematian       Statistik Kesehatan
Statistik Perusahaan       Statistik Jam Lembur
Statistik Pertanian       Statistik Kecelakaan, dll.

Statistik Pendidikan
di Kelurahan: …………..    bulan:    Agustus 2000
Jenjang   Laki-laki   Wanita   Jumlah
SD
SLP
SLA
UNIV

Statistik Penduduk
di Jakarta: …………..    bulan:    Agustus 2000
Walikota   Laki-laki   Wanita   Jumlah
JakPus
JakTim
Jakbar
JakSel

Statistik Nilai Ujian
Mata Kuliah: ………….. Semester: …..

Nilai
Ujian
Kode   Jumlah
Mahasiswa
0 – 44   E
45 – 55   D
56 – 61   C
62 – 67   C+
68 – 73   B
74 – 79   B+
80 – 100   A

Statistik Jam Lembur:
Banyaknya jam lembur tiap minggu oleh pekerja-pekerja suatu pabrik adalah:
45   31   46   25   57   39   42   55   20   37
   40   59   11   38   34   22   62   33   48   43
   57   37   43   51   29   41   35   66   45   32
   44   47   42   46   54   65   17   35   53   27
   38   22   33   39   45   32   43   41   57   45

Statistik Jam lembur dalam data berkelompok:
Perusahaan: ………..

Jam
Lembur
Turus   Jumlah
Pegawai
10 – 19   //   2
20 – 29   //// /
6
30 – 39   //// //// ////
14
40 – 49   //// //// //// //
17
50 – 59      //// ///
8
60 – 69   ///   3

PENYAJIAN DATA

Diagram dan Grafiks

1. Diagram batang
2. Diagram garis / grafiks ( lurus / patah / lengkung )
3. Diagram Lambang
4. Diagram lingkaran
5. Diagram Peta
6. Diagram pencar / titik

	agustiannnn pada MATEMATIKA DASAR : BAB 10
	mnazaruddinsyafiq pada MATEMATIKA DASAR : BAB 10
	agustiannnn pada BAB 5
	agustiannnn pada BAB 6
	agustiannnn pada KEWIRAUSAHAAN : BAB 4

AGUSTIAN

Kumpulan Modul dan Materi Perkuliahan Ilmu Komputer

Category Archives: Statistika dan Probabilitas

STATISTIKA DAN PROBABILITAS : BAB 10

STATISTIKA DAN PROBABILITAS : BAB 9

STATISTIKA DAN PROBABILITAS : BAB 8

PROBABILITAS (PELUANG KEJADIAN)

KOMBINASI (urutan tidak diperhatikan ®Tidak perlu ada tempat duduk )

PERMUTASI (urutan diperhatikan ® Ada tempat duduk )

STATISTIKA DAN PROBABILITAS : BAB 7

STATISTIKA DAN PROBABILITAS : BAB 6

Trend Kwadratic (Parabola)

STATISTIK DAN PROBABILITAS : BAB 5

STATISTIKA DAN PROBABILITAS : BAB 4

A2. INDEX GABUNGAN

STATISTIKA DAN PROBABILITAS : BAB 3

STATISTIKA DAN PROBABILITAS : BAB 2

STATISTIKA DAN PROBABILITAS : BAB 1

Statistik Pendidikan

Statistik Penduduk

Statistik Nilai Ujian

Statistik Jam lembur dalam data berkelompok:

PENYAJIAN DATA